M344: Calculus III
Section 16.4
In this section we will discuss a remarkable theorem known as Green's theorem. But first we need to gather some definitions.
Definition¶
A simple closed curve, also known as a Jordan curve, is a curve in the plane that has no endpoints and no self-intersections. You can think of a Jordan curve as being obtained by continuously deforming a circle.
Examples¶
Here is an image from our textbook that illustrates the differences between simple, not simple, closed, and not closed.
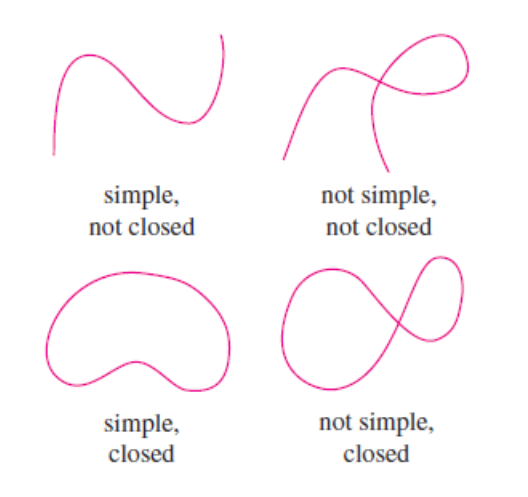
Some History
Jordan curves are named after the mathematician Camille Jordan, whose name is also attached to an infamous theorem.
The Jordan Curve Theorem
Every Jordan curve divides the plane into two disjoint regions: one bounded, and one unbounded.
The bounded region is called the interior of the curve, and is frequently referred to as a Jordan region. This theorem is infamous not for the difficulty of its statement. It's actually rather easy to visualize a picture of this theorem in your mind. However, it turns out that it was very hard to prove. In fact, Jordan's original proof was wrong! Years later, a mathematician named Oswald Veblen gave a corrected proof. But Jordan still got to keep his naming rights.
Definition¶
A Jordan curve is said to be positively oriented if as it's traversed, the bounded interior region is on the left.
Here is another image from our textbook illustrating the difference between positive and negative orientation of a Jordan curve.
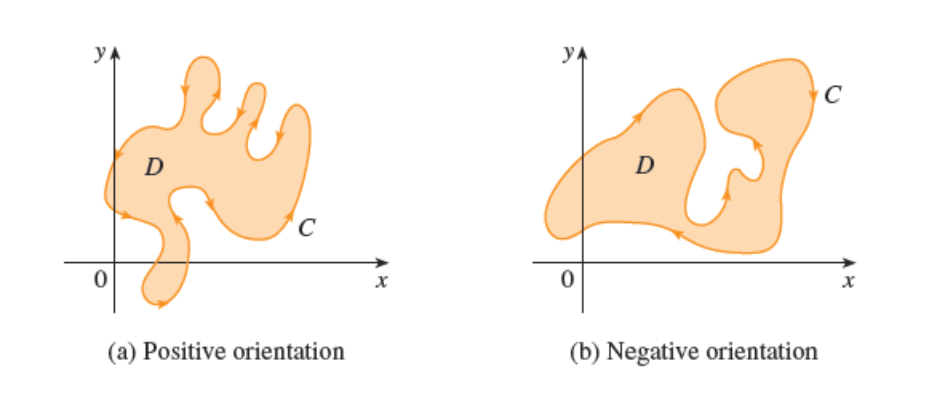
We are now ready to state the main theorem of this section.
Green's Theorem¶
Let $C$ be a positively-oriented, piecewise-smooth Jordan curve in the plane, and let $D$ denote the bounded region enclosed by $C$. Let $\mathbf{F}(x,y) = \langle P(x,y), Q(x,y) \rangle$ be a vector field such that $P$ and $Q$ have continuous first derivatives on an open region containing $D$. Then
$$
\int_C \mathbf{F}\cdot d\mathbf{r} = \int\!\!\!\!\int_D \left(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right)\, dA.
$$
Video lecture
We prove a special case of this theorem, when the region $D$ is a particularly nice region.
Video proof
1. Example¶
Use Green's theorem to evaluate $\int_C \mathbf{F}\cdot d\mathbf{r}$ where
$$
\mathbf{F} = \big(e^{-x} + y^2\big) \,\mathbf{i} + \big(e^{-y} + x^2 \big)\,\mathbf{j},
$$
and $C$ consists of the arc of the curve $y = \cos x$ from $\big(-\frac{\pi}{2},0\big)$ to $\big(\frac{\pi}{2},0\big)$ and the line segment from $\big(\frac{\pi}{2},0\big)$ to $\big(-\frac{\pi}{2},0\big)$.
Video solution
2. Example¶
Compute the work done by the force
$$
\mathbf{F} = \langle x(x+y),xy^2 \rangle
$$
in moving a particle from the origin along the $x$-axis to $(1,0)$, then along the line segment tp $(0,1)$, then back to the origin along the $y$-axis.
Video solution
3. Example¶
Show that if $C$ is the line segment connecting the point $(x_1,y_1)$ to the point $(x_2,y_2)$, show that
$$
\int_C x\,dy - y\, dx = x_1y_2 - x_2y_1.
$$
Then use this fact together with Green's theorem to compute the area of a polygon with vertices $(x_1,y_1)$, $(x_2,y_2)$, ..., $(x_n,y_n)$, in the positive counter-clockwise orientation.
Your answer is called the shoelace formula for computing the area of a polygon. You might remember this from a high school geometry class.
Video solution
Extended Green's Theorem¶
We have only proved in the case when the region $D$ can be represented as both type I and type II, depending on our preference. However, Green's theorem does hold when $D$ is any Jordan region.
Actually, the conclusion of Green's theorem continues to hold when our region is bounded by a finite disjoint union of Jordan curves.
Video lecture
4. Example¶
Calculate the path integral $\int_C \mathbf{F}\cdot d\mathbf{r}$ where
$$
\mathbf{F}(x,y) = \frac{2xy\,\mathbf{i} + (y^2 - x^2)\,\mathbf{j}}{(x^2 + y^2)^2}
$$
and $C$ is any positively-oriented Jordan curve that encloses the origin.
Video solution
We'll conclude these notes by finishing a proof that we left in section 16.3. Recall the theorem,
Theorem¶
Let $\mathbf{F} = \langle P, Q \rangle$ be a vector field on an open simply connected region $D$, such that $P$ and $Q$ both have continuous first-order partial derivatives in $D$. Then $\mathbf{F}$ is conservative if and only if
$$
\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} = 0
$$
at every point in $D$.
We've already proved the direction in which we get to assume that $\mathbf{F}$ is conservative. Only the converse remains. Try to prove this yourself before watching the video. If you've worked through these entire notes, the proof should be screaming at you.
Video proof
Note: In the video below I have inadvertently left off the assumption that $D$ be an open region. In what step of the proof did I use this (un-stated, but necessary) assumption?
Discussion¶
Questions? You can ask them here.