M344: Calculus III
Section 16.2
Path Integrals¶
A note to the reader
Our textbook calls the main objects of study in this section "line integrals." When I first learned Calculus III, I called them by this name as well. But over the years I have convinced myself that this name is unnecessarily misleading. At some point in my past (probably under the influence of my PhD advisor), I began replacing the book's four-letter word with a different four-letter word, and started calling these objects "path integrals."
I believe that this simple, and seemingly stupid, change in nomenclature makes a net-positive difference in the way that we think about and understand what these objects are actually doing, geometrically. For this reason, I will unapologetically always refer to line integrals as path integrals for the remainder of this semester, and probably eternity.
Suppose $C$ is a curve in $\mathbb{R}^n$, and let $f$ be a function defined on a domain $D$ that contains the curve $C$. In this section, we will consider the restriction of the function $f$ to the curve $C$. The situation is illustrated for $C \subset \mathbb{R}^2$ in the image below.
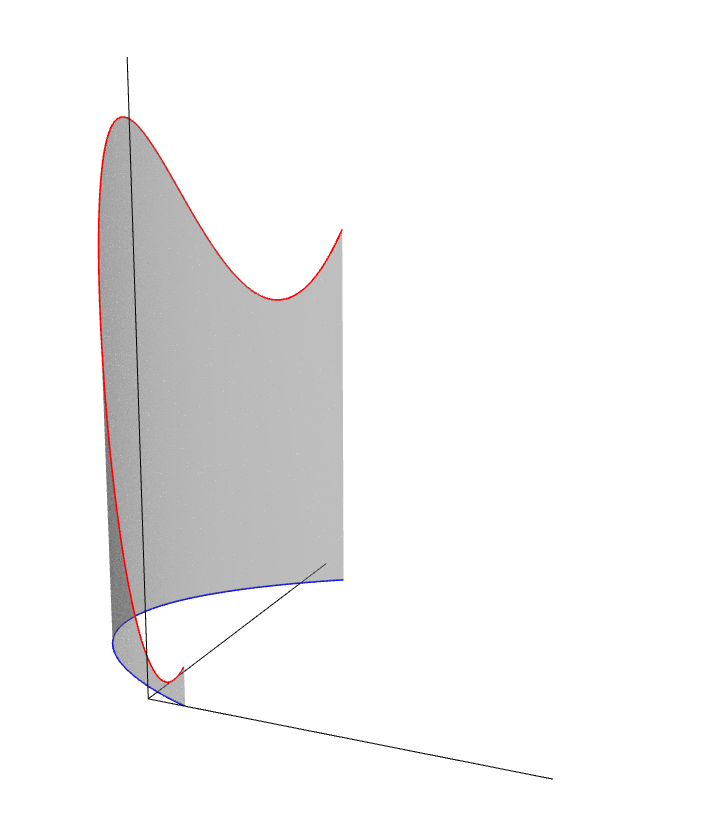
The path integral of $f$ along $C$ is defined to be the surface area of the surface defined by $C$ and $f(C)$. To compute this area, we may use any parametrization of the curve $C$. However, the choice of parametrization cannot effect the value of the integral. The path integral is a geometric quantity that depends only on the path $C$, and not on the speed at which $C$ is traversed. Therefore we must integrate the function $f$ with respect to arclength along $C$.
Video lecture
</details
Definition¶
Let $C$ be a path in $\mathbb{R}^n$ parametrized by a vector function $\mathbf{r}$ on an interval $[a,b]$, and suppose $f$ is a function defined on a set containing $C$. The path integral of $f$ along $C$ is
$$
\int_C f(\mathbf{x})\,ds = \int_a^b f\big(\mathbf{r}(t)\big)\, \Vert \dot{\mathbf{r}}(t) \Vert\, dt.
$$
1. Example¶
Evaluate the path integral
$$
\int_C \frac{y}{x}\,ds,
$$
where $C$ is the portion of the circle $x^2 + y^2 = 16$ bounded between the rays $\theta = 0$ and $\theta = \frac{\pi}{4}$ (in this orientation) in polar coordinates.
Check your answer
$$\ln 4$$
Video solution
2. Example¶
Evaluate the path integral
$$
\int_C xe^{yz}\,ds
$$
where $C$ is the line segment from $(0,0,0)$ to $(1,2,3)$.
Check your answer
$$\frac{\sqrt{14}\,\big(5e^6 + 1\big)}{36}$$
Video solution
Partial Path Integrals¶
Now that we're beginning to understand how path integrals work, we can start to modify the situation. Instead of integrating a function along a path with respect to arclength, we can integrate the function with respect to infinitesimal changes in the coordinate directions. These integrals no longer carry the geometric intuition of computing a surface area. We'll discuss one physical interpretation of these integrals later in the notes.
The resulting integrals are called partial path integrals.
3. Example¶
Evaluate the path integral
$$
\int_C \Big(\big(y+z\big)\,dx + \big(x+z\big)\,dy + \big(x+y\big)\,dz\Big),
$$
where $C$ consists of the line segments from $(0,0,0)$ to $(1,0,1)$, and then from $(1,0,1)$ to $(0,1,2)$.
Check your answer
$$2$$
Video solution
Path Integrals of Vector Fields¶
We began Chapter 16 by defining and studying vector fields. Now we would like to integrate a vector field along a curve. We begin this discussion by drawing motivation from a physics problem.
4. Motivating Example: Work¶
Suppose a particle is moving in space along a path $C$. Simultaneously, the particle is being acted on by a vector field $\mathbf{F}$. Derive a formula for the total work done by the vector field on the particle as it moves from point $A$ to point $B$ along the path.
Video lecture
Definition¶
The work done by a vector field $\mathbf{F}$ on a particle traversing a path $C$ is given by
$$
\text{Work} = \int_C \mathbf{F}\cdot d\mathbf{r},
$$
where $\mathbf{r}$ is any parametrization of $C$. If the path is traversed from $\mathbf{r}(a) = A$ to $\mathbf{r}(b) = B$, then the path integral is given by
$$
\int_C \mathbf{F}\cdot d\mathbf{r} = \int_a^b \mathbf{F}\big(\mathbf{r}(t)\big)\cdot \dot{\mathbf{r}}(t)\, dt.
$$
Moreover, if the vector field is decomposed into component functions,
$$
\mathbf{F}(x,y,z) = \big\langle P(x,y,z), Q(x,y,z),R(x,y,z) \big\rangle,
$$
and $\mathbf{r}(t) = \langle x(t), y(t), z(t) \rangle$, then the path integral is given by
$$
\begin{align}{}
\int_C \mathbf{F}\cdot d\mathbf{r} & = \int_A^B \Big( P(x,y,z)\, dx + Q(x,y,z)\, dy + R(x,y,z)\, dz \Big) \\[2ex]
& = \int_a^b \Big( P\big(x(t),y(t),z(t)\big)\, \dot{x}(t) + Q\big(x(t),y(t),z(t)\big)\, \dot{y}(t) + R\big(x(t),y(t),z(t)\big)\, \dot{z}(t) \Big)\, dt
\end{align}
$$
Exercise¶
Work out all of the details in these derivations. What changes if the curve and vector field live in $\mathbb{R}^2$ instead of $\mathbb{R}^3$?
5. Example¶
Consider the force field
$$
\mathbf{F}(x,y) = \big\langle x^2, xy \big\rangle
$$
acting on a particle that travels once around the circle $x^2 + y^2 = 4$, in the positive orientation. Compute the work done by $\mathbf{F}$ on this particle. Interpret your answer. Does it make sense?
Check your answer
$$0$$
Video solution
Discussion¶
Questions? You can ask them here.