Parametrized Curves¶
A parametrized curve is a curve given by the graph of a parametric function; that is, a function $f :\mathbb{R} \to \mathbb{R}^2$ defined by
$$
f(t) = \begin{cases} x = x(t), \\ y = y(t). \end{cases}
$$
Since we've already studied vectors in Chapter 12, we can write this parametric function in vector notation. The convention when doing this is to change the "name" of the function from $f$ to $\mathbf{r}$. We write
$$
\mathbf{r}(t) = \left\langle x(t),y(t) \right\rangle.
$$
Regardless of how we choose to write parametric functions, we need to understand how they trace out curves. This is the topic of the next video.
Video lecture
1. Examples¶
In the following video we plot the graphs of each of the following parametric functions.
- $f(t) = \displaystyle \begin{cases} x = t, \\ y = t^2 \end{cases}$
- $g(t) = \displaystyle \begin{cases} x = e^t, \\ y = e^{2t} \end{cases}$
- $h(t) = \displaystyle \begin{cases} x = \sin(t), \\ y = \sin^2(t) \end{cases}$
Before you watch the video, try to work out what each curve looks like. How are they related? How do they differ?
Video lecture
2. Exercise¶
Find a parametric function (or a set of parametric functions) for the circle with center $(h,k)$ and radius $r > 0$.
Solution
First, the Cartesian equation of the circle is $(x-h)^2 + (y-k)^2 = r^2$.
There are many ways to parametrize this circle. One way is to make the substitutions
$$
\begin{align}
u & = \dfrac{x-h}{r}, \\[0.5 ex]
v & = \dfrac{y-k}{r}.
\end{align}
$$
Then the equation becomes $r^2u^2 + r^2 v^2 = r^2$, or simply $u^2 + v^2 = 1$. This equation represents a unit circle, so we can use trigonometry to parametrize it. We set
$$
f(t) = \begin{cases} u = \cos(t), \\ v = \sin(t). \end{cases}
$$
Subbing back in for $u$ and $v$ and then solving for $x$ and $y$ gives the parametric function
$$
f(t) = \begin{cases} x = h + r\cos(t), \\ y = k + r\sin(t). \end{cases}
$$
Notice that this parametric fuction traces out the circle exactly once on the interval $0 \leq t < 2\pi$.
3. Exercise¶
Use a substitution similar to the one used in the previous exercise to find a parametrization of the ellipse
$$
9x^2 + 16y^2 = 144.
$$
Check your answer
One solution is
$$
\mathbf{r}(t) = \left\langle 4\cos t, 3\sin t \right\rangle.
$$
4. Example¶
The Witch of Agnesi is the curve defined to be the locus of all points $P$ defined by the image below.
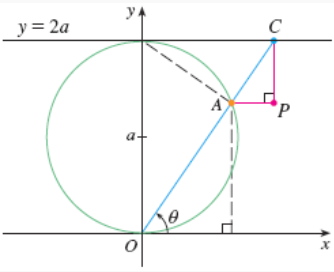
Find parametric equations for the point $P$ in terms of the angle $\theta$ in the image.
Check your answer
$$
P(\theta) = \begin{cases}
x = 2a\cot\theta \\
y = 2a\sin^2\theta
\end{cases}
$$
Video solution
The Cycloid¶
One important example of a parametric curve that we will see frequently in applications and examples moving forward is the cycloid. The cycloid is the shape of a curve that is traced out by a fixed point on a circle of radius $r$, as the circle "rolls" along the $x$-axis. We derive the parametric equations in the next video.
Video lecture
Parametric equations for the cycloid
$$
\begin{cases}
x(\theta) = r(\theta - \sin\theta), \\[0.5ex]
y(\theta) = r(1 - \cos\theta), \\[0.5ex]
\theta \in \mathbb{R},\ \ r>0\ \text{constant}.
\end{cases}
$$
5. A Beautiful Application¶
We'll end these notes with a beautiful example of the cycloid in nature. The following YouTube video is by a channel called 3 Blue 1 Brown. We'll see lots more videos by this channel over the weeks to follow. In this video, they explore the origins of the famous Bachristochrone problem, and talk about its solution. Enjoy!
The Bachristochrone Problem
</details>
Discussion¶
Questions? You can ask them below.